Kuhn poker is an extremely simplified form of poker developed by Harold W. Kuhn as a simple model zero-sum two-player imperfect-information game, amenable to a complete game-theoretic analysis. In Kuhn poker, the deck includes only three playing cards, for example a King, Queen, and Jack. One card is dealt to each player, which may place bets similarly to a standard poker. If both players bet or both players pass, the player with the higher card wins, otherwise, the betting player wins.

• Important: We use Google's reCaptcha service to protect our free calculators against automated requests. By using this calculator you agree that Google will analyze data about your browsing session to help us verify that you are a human user.
• Nash Equilibrium In Texas Holdem What many people don’t know is Nash Equilibrium In Texas Holdem that playing with a good and fair deposit bonus gives you a much, much higher chance of leaving the games with a profit, and bonuses are by far the biggest Nash Equilibrium In Texas Holdem cost of any online casino.
• Powerful poker tools and mathematical models have have enabled poker players to develop and implement game-theory based unexploitable and optimal poker strategies and plays in specific, key situations. One concept which is highly applicable to poker tournaments and SNGs is 'Nash Equilibrium'.

Game description[edit]

Provide a phenomenal array of online casino games; Have large casino bonuses and other fantastic online casino promotions for Nash Equilibrium Poker US players that are regulated for safe and easy.

Nash Equilibrium Poker

In conventional poker terms, a game of Kuhn poker proceeds as follows:

• Each player antes 1.
• Each player is dealt one of the three cards, and the third is put aside unseen.
• Player one can check or bet 1.
  • If player one checks then player two can check or bet 1.
    • If player two checks there is a showdown for the pot of 2 (i.e. the higher card wins 1 from the other player).
    • If player two bets then player one can fold or call.
      • If player one folds then player two takes the pot of 3 (i.e. winning 1 from player 1).
      • If player one calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).
  • If player one bets then player two can fold or call.
    • If player two folds then player one takes the pot of 3 (i.e. winning 1 from player 2).
    • If player two calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).

Optimal strategy[edit]

The game has a mixed-strategyNash equilibrium; when both players play equilibrium strategies, the first player should expect to lose at a rate of −1/18 per hand (as the game is zero-sum, the second player should expect to win at a rate of +1/18). There is no pure-strategy equilibrium.

Kuhn demonstrated there are infinitely many equilibrium strategies for the first player, forming a continuum governed by a single parameter. In one possible formulation, player one freely chooses the probability${\displaystyle \alpha \in [0,1/3]}$ with which he will bet when having a Jack (otherwise he checks; if the other player bets, he should always fold). When having a King, he should bet with the probability of ${\displaystyle 3\alpha }$ (otherwise he checks; if the other player bets, he should always call). He should always check when having a Queen, and if the other player bets after this check, he should call with the probability of ${\displaystyle \alpha +1/3}$.

The second player has a single equilibrium strategy: Always betting or calling when having a King; when having a Queen, checking if possible, otherwise calling with the probability of 1/3; when having a Jack, never calling and betting with the probability of 1/3.

Generalized versions[edit]

In addition to the basic version invented by Kuhn, other versions appeared adding bigger deck, more players, betting rounds, etc., increasing the complexity of the game.

3-player Kuhn Poker[edit]

A variant for three players was introduced in 2010 by Nick Abou Risk and Duane Szafron. In this version, the deck includes four cards (adding a ten card), from which three are dealt to the players; otherwise, the basic structure is the same: while there is no outstanding bet, a player can check or bet, with an outstanding bet, a player can call or fold. If all players checked or at least one player called, the game proceeds to showdown, otherwise, the betting player wins.

A family of Nash equilibria for 3-player Kuhn poker is known analytically, which makes it the largest game with more than two players with analytic solution.^[1] The family is parameterized using 4–6 parameters (depending on the chosen equilibrium). In all equilibria, player 1 has a fixed strategy, and he always checks as the first action; player 2's utility is constant, equal to –1/48 per hand. The discovered equilibrium profiles show an interesting feature: by adjusting a strategy parameter ${\displaystyle \beta }$ (between 0 and 1), player 2 can freely shift utility between the other two players while still remaining in equilibrium; player 1's utility is equal to ${\displaystyle -\frac{1+2\beta }{48}}$ (which is always worse than player 2's utility), player 3's utility is ${\displaystyle \frac{1+\beta }{24}}$.

It is not known if this equilibrium family covers all Nash equilibria for the game.

References[edit]

• Kuhn, H. W. (1950). 'Simplified Two-Person Poker'. In Kuhn, H. W.; Tucker, A. W. (eds.). Contributions to the Theory of Games. 1. Princeton University Press. pp. 97–103.
• James Peck. 'Perfect Bayesian Equilibrium'(PDF). Ohio State University. Retrieved 2 September 2016.^:19–29

1. ^Szafron, Duane; Gibson, Richard; Sturtevant, Nathan (May 2013). 'A Parameterized Family of Equilibrium Profiles forThree-Player Kuhn Poker'(PDF). In Ito; Jonker; Gini; Shehory (eds.). Proceedings of the 12th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2013). Saint Paul, Minnesota, USA.

External links[edit]

By: James McNamara & Anmol Srivats

Nash equilibrium is defined as a state in a multi-player game where every player knows every other player’s strategy and no player has any incentive to change his or her own strategy. This concept may seem purely academic, since it explains something that we already understand, but in addition to a way of formalising the intuitions we all have about human behaviour inside economic theory, the concept has also been responsible for changes in the way we think about the real world.

Applying this concept to real world cases makes it tangible. For example, in the game of poker there are real profits to be made by simply following strategies that minimize the deviation in your own play from ‘perfect’ Nash equilibrium. To push that out of the realms of abstract game theory, think of this strategy as exploiting someone by attacking their weaknesses, and when opponents’ skills increase to the point that they no longer have weaknesses, your best option is to remove your own weaknesses so as to not be exploitable.

Within online poker (which removes elements such as tells), there are two ways to denominate every strategy – exploitable and exploitative. Exploitable strategies are ones that deviate from the Nash equilibrium, while exploitative strategies deviate from Nash specifically to exploit opponents’ exploitable strategies. By definition, exploitative strategies must always deviate less from Nash than exploitable strategies, otherwise they would be exploitable strategies. Therefore under certain conditions, the optimal strategy is more about not being exploited than about exploiting the weaknesses of others. Closely following Nash equilibrium becomes a fairly strong exploiting strategy, and by definition, following ‘perfect’ Nash is a non-exploitable strategy.

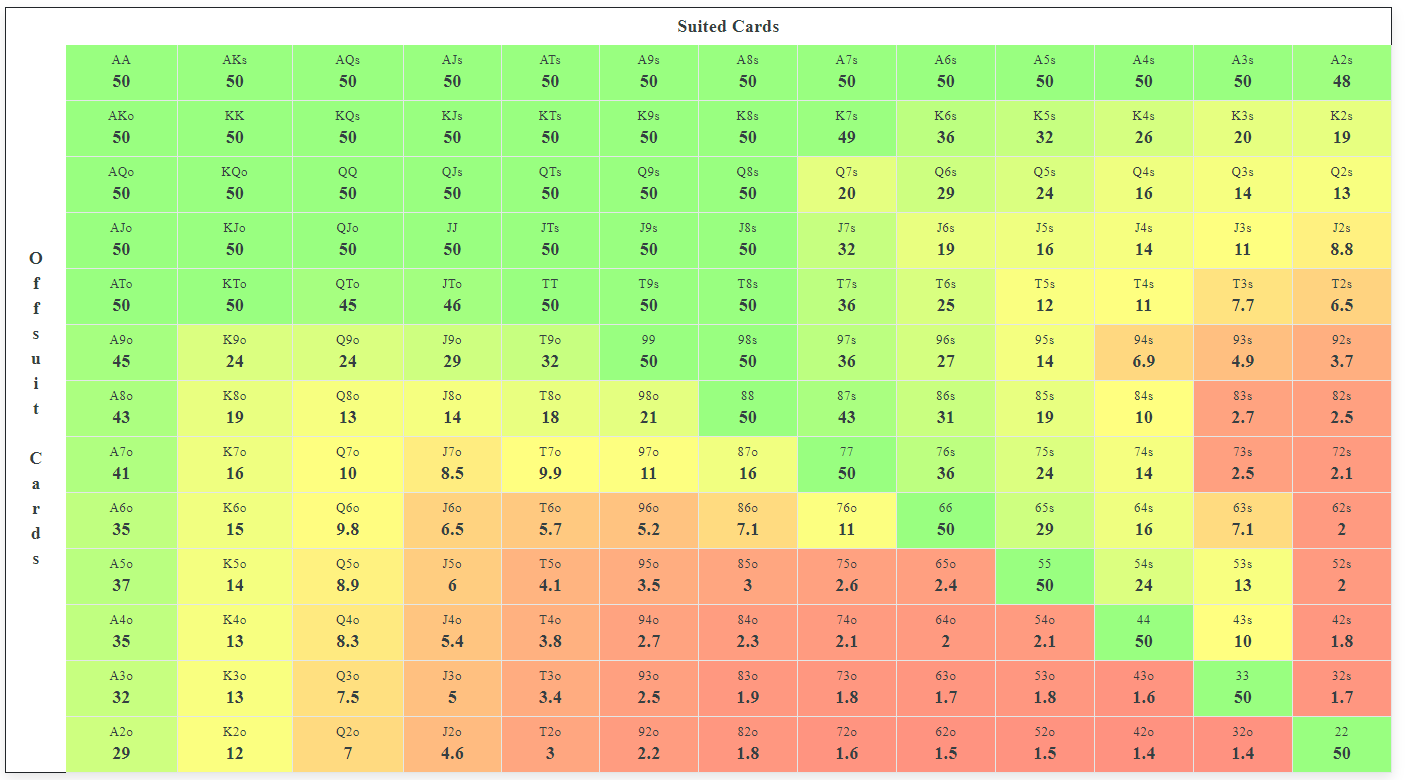
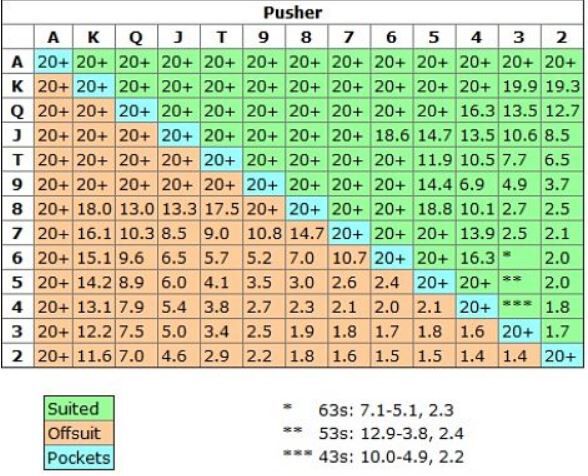
Nash Equilibrium Shove Fold Chart

A trivial application of this reasoning can be seen in bluffs and calls. If another player bluffs very often when he bets, you will call very often. Suppose that some reason – perhaps he is trying to impress a lady friend – he knows that you will call, but still perceives it to be in his best interest to continue his strategy. Thus neither of you would opt to change your strategy: he would continue to bluff, and you would continue to call. Since the strategies don’t change, they are in a static state – i.e., they are in equilibrium.

The strategies sound simple enough, but the calculation of Nash equilibrium is not. When two people play a hand of online poker, the number of possible combinations of cards that can be dealt equals 5.56*10^13. To obtain Nash equilibrium, you need to compute each of these combinations as well as decide things such as the optimal bet size on each of four betting rounds. Altogether, these decisions would push the exponent well beyond 10^20. In addition, you may be playing games with six or nine players at your table, which would increase the number of card combinations to 2*10^25 and 3*10^33 respectively. Because the number of card combinations and the number of betting combinations are so high, no computer will find the Nash equilibrium of poker any time soon. Thus, the best players in the world have to estimate the Nash equilibrium, and compete between their estimations.

Interestingly, online variations of the standard poker format, such as ‘Hyper-Turbo’ tables, create a more rigid structure of the game in which Nash strategy is not only easier to follow but, with practice, can reward clever players. The game starts with four players each holding a stack consisting of 10 big blinds (as opposed to regular games, which are 100 big blinds deep), and the blinds double every 3 minutes, meaning that a typical tournament lasts only 5 minutes. Due to the short stack sizes, there is not much play after the flop in the games, and the vast majority of players’ decisions are either ‘all in’ or ‘fold’ before the flop is dealt. Since we have a good idea of the probability of two hands beating each other in a pre-flop scenario, and since decisions are binary (all in or fold), it is easier to estimate a Nash equilibrium for these games than for standard games. In addition, because the Nash equilibrium is relatively easy to calculate, most players are not playing particularly exploitable strategies so your edge is relatively small resulting in a large variance. However, since you will play a large number of games, this variance becomes unimportant. Over time, the strength of your conformity to Nash will ultimately determine your success and earning potential.

Nash Equilibrium In Economics

Since the number of decisions is limited to two for all players, the card combinations are limited to one of 169 hands (suited, off-suit, and pairs), and generally only two players go all in against each other at once, a Nash equilibrium estimate requires going through a ‘mere’ 600,000 combinations, which a computer can do reasonably quickly. Thus it is possible to study and better yourself at this variation of poker with the help of software, which is easily available by Googling ‘ICM Nash calculator’.

Nash Equilibrium Examples

Successful application of this simple economic concept – combined with dedication and a sliver of luck – can be profitable, especially on higher stakes tables where both risks and rewards escalate.